Probability as Area under the curve
Discrete Space Sample
One Dice Experiment
Let us consider the experiment of throughing one dice. The sample space is {1,2,3,4,5,6}. Assuming a fair dice, the probability of getting any of these numbers is 1/6. Since all of the probabilities are the same, we can say that we have a Uniform Probability. We can also depict this probability in the following figure.

(source)
Two Dice Experiment
We can compare that to the 2 dice experiment. If we are interested in the sum of the two dice, the sample sapce becomes {2,3,4,5,6,7,8,9,10,11,12}. But the probability of that sum to occur is not uniform. The following figure shows the odds/probability of each sum. That probability is cuculated by counting the numbers of ways a certain some can occur divided by the total numbers of possiblities, 36 in this case. The figure below shows how we can calculate these odds and in how many ways each sum might be obtained.

(source)
If we wanted to calculate the probbility of getting a sum less or equal to 5, that can be represented by the sum of the probabilities or the red area in the figure below.

Continuous Sample Sapce
In both examples above we considered a discrete sample space. That means we can "count" the number of outputs. But we can also have a continuous sample space. In that case, we do not talk about probability, but rather a probability desity funcion, PDF. And the probability becomes the area under that curve. For example, for a a continuous uniform proability density function, similar to the single dice problem, we write:
 (Source)
(Source)Note that the area under the curve in this case is (d-c)*(1/(d-c)) = 1. That condition has to be satisfied all the time.
Exmaple:

(Source)
Exmaple:
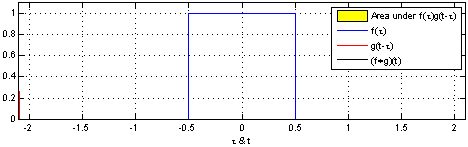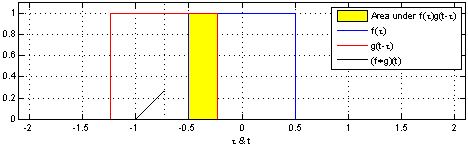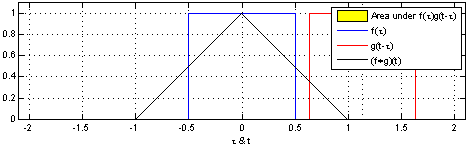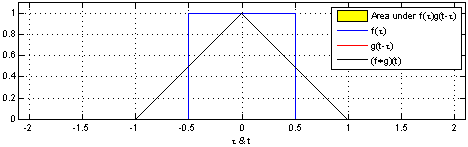
Consider the following experiment. Two people are traveling throught the same airport. Each has a layover of time T, could be an hour, more or less. Their plans arrive at the airport at random times. What is the probability of these two people meet at the airport as a function of the difference of the arrival time of one plane with respect to the other?
The Standard Normal Distribution
The most common example of a continuous Probability Density Function, PDF, is the standard normal distribution. That is a distribution with zero mean and sigma = 1. The PDF and Cumulative Distribution Fucntion are shown in the figure below. These are standard figures. But we can also view an animation of how this CDF is getting calculated here.
Other PDFs
Exponential PDF

(Source)
Wind Speed

(Source)
Refs:
Convolution of two square functions.